Solving the math puzzle of the Schönbrunn maze in Vienna

Introduction

There is a castle in Vienna called Schönbrunn. You may have heard about it because it is quite famous thanks to the Empress Elisabeth of Austria, a.k.a princess Sisi.

In the garden, there are several mazes, like this:

In one of the mazes, there is a puzzle, made of tiles that are put on the ground. It looks like this:

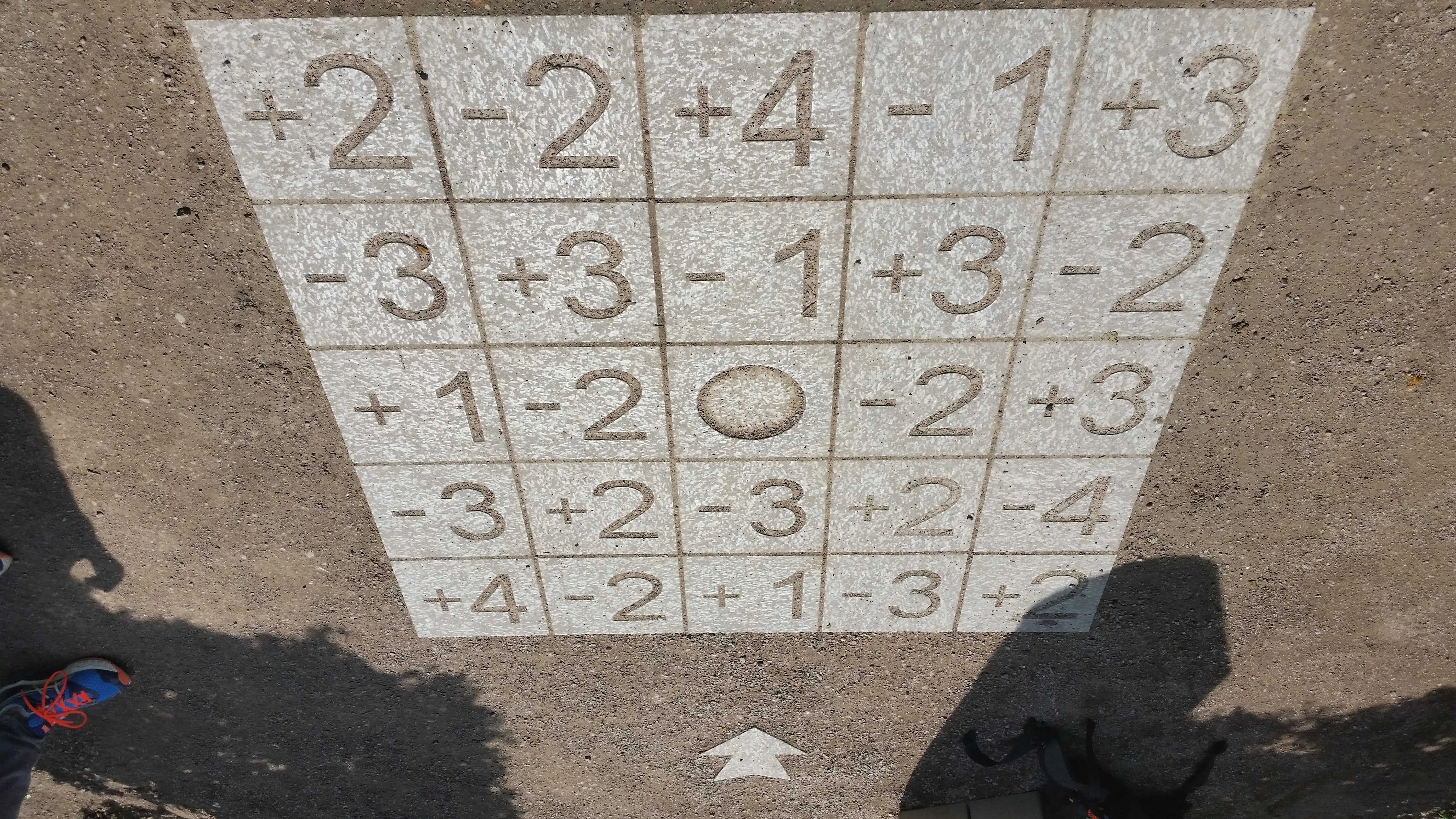
It is a good brain teaser for tourists passing by, as they can even step on the tiles to find the solution.

Rules

• There are two difficulties: normal and expert.
• Start from the arrow. It means that the first tile to step on is the tile +1.
• The number you step on indicates the number of steps you can take in any of the 4 directions: up, left, right, down. However, it is not possible to jump outside the grid (you should stay within the boundaries).
• You jump from tile to tile until you reach the tile in the center, the O.
• You can jump on a tile only once.
• Normal mode: reach the O in the center, ignoring the positive and negative signs.
• Expert mode: reach the O in the center, but the sum of the visited tiles must be equal to 0 in the end.

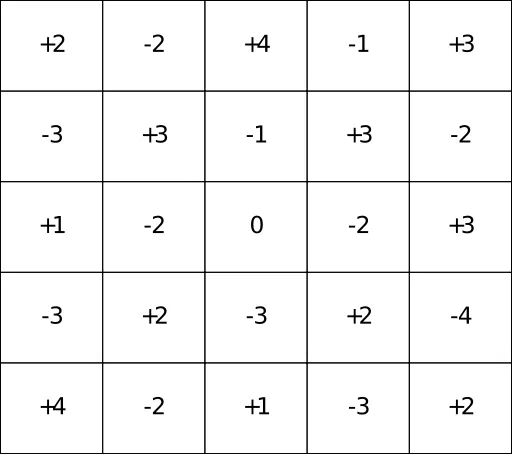
Here is a blank version of the puzzle, that you can print or copy on a piece of paper.

Example

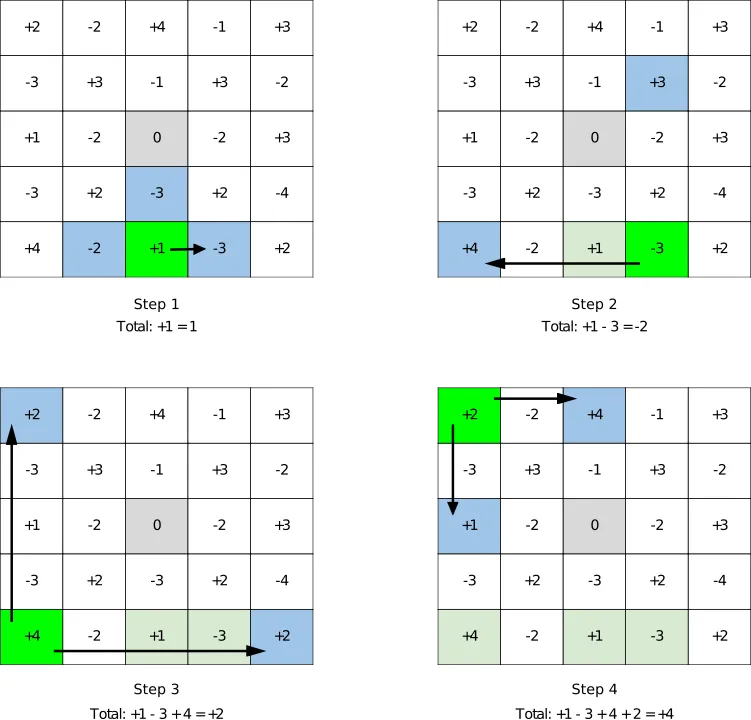
Here is a list of steps arbitrarely chosen to serve as an example:

1. Start on +1. We can move 1 step up, left or right, but not down because it is out of the grid.
2. Go right, on -3. From this tile, we can go up (+3) or left (+4)
3. Go left, on +4. From this tile we can go up (+2) or right (+2)
4. Go up, on +2. From this tile we can go down (+1) or right (+4)
5. …

Solution

By hand

This puzzle is meant to be solved by hand (or by foot as it is possible to stand on the tiles). There might be different approaches to the problem.

Let’s consider the top left corner (the tile +2) to be the origin of the grid, (0,0).

One possible solution is to approach it like for regular mazes: start from the end. For each tile, look around to see from what other tile we can reach the one we are currently standing on. Starting from the middle, there is only one tile that works: the -1 above. So the predecessor of the end tile (2, 2) is (2, 1). Then from (2, 1), the question is the same: how did we get there, from the top, bottom, left or right?

• from the top: impossible, as the tile is 4 (too big)
• from the bottom: impossible, as the tile are 1 (too small) or 3 (too big)
• from the left: impossible, as the tiles are 3 and 3 (too big).
• from the right: there is one candidate!, -2, because by jumping two tiles on the left from there (2, 3), we end up on our current (2, 1)

Then the new current tile is (2, 3). Repeat the same logic. When there is more than one possibility, pick one and continue. If in the end it doesn’t work, go back to the point where you made the choice and try the next option (backtracking).

By proceeding like this, you will eventually reach the end (actually the entrance).

With a program

We just saw how to solve it “manually”, but it is also possible to find the solution(s) with a program.

The puzzle can be expressed as a graph problem, by defining a set of nodes and edges iterate through them.

The idea is to use a similar approach as a DFS, but not stopping at the first solution found. In that case, the sum could be different than 0. We want to find the best solution, that solves the expert mode in the least amount of steps.

Here is a Python implementation with comments that gives an answer. I also turned it into a gist: https://gist.github.com/jtpio/f4175e0c38d2be4b44c9

# read the input from a file
n, m = [int(c) for c in input().split(' ')]
sx, sy = [int(c) for c in input().split(' ')]
ex, ey = [int(c) for c in input().split(' ')]

# utilities to convert coordinates to vertex id and vice versa
def coord_to_id(i, j):
    return i * m + j

def id_to_coord(x):
    return (x // m, x % n)

# store the grid
g = [ [int(c) for c in input().split(' ')] for _ in range(n)]

# build the graph
graph = {}
for i in range(n):
    for j in range(m):
        # read how many steps can be taken
        steps = abs(g[i][j])
        if steps == 0:
            continue
        x = coord_to_id(i, j)
        # define the list of neighbors
        graph[x] = []
        # from the current tile x, jump "steps" tile up, left, down, right
        if i - steps >= 0:
            graph[x].append(coord_to_id(i-steps, j))
        if i + steps < n:
            graph[x].append(coord_to_id(i+steps, j))
        if j - steps >= 0:
            graph[x].append(coord_to_id(i, j-steps))
        if j + steps < m:
            graph[x].append(coord_to_id(i, j+steps))

start = coord_to_id(sx, sy)
end = coord_to_id(ex, ey)

# store all the solutions
paths = []
# backtrack a solution
prev = {}
visited = set()
prev[start] = None

# called dfs, but is actually a complete search
def dfs(u):
    if u == end:
        a = end
        p = []
        while a != None:
            p.append(a)
            a = prev[a]
        paths.append(p)
        return
    for v in graph[u]:
        if v not in visited:
            visited.add(v)
            prev[v] = u
            dfs(v)
            # complete search: pretend this path was not explored
            # to consider it later
            visited.remove(v)

# search
visited.add(start)
dfs(start)

# results
solutions = []
for p in paths:
    tiles = [id_to_coord(tile) for tile in p[::-1]]
    s = sum([g[x[0]][x[1]] for x in tiles])
    # log all the solutions
    solutions.append((s, len(tiles), tiles))

# find the best
best = min(solutions, key=lambda s: (abs(s[0]), s[1]))
print('The best solution is a sum of', best[0], 'in', best[1], 'steps.')
sol = ' -> '.join([str(c) + ', tile ' + str(g[c[0]][c[1]]) for c in best[2]])
print(sol)

Which outputs the solution:

The best solution is a sum of 0 in 15 steps:
(4, 2), tile 1 -> (4, 1), tile -2 -> (2, 1), tile -2 -> (2, 3), tile -2 -> (4, 3), tile -3 -> (4, 0), tile 4 -> (0, 0), tile 2 -> (2, 0), tile 1 -> (3, 0), tile -3 -> (3, 3), tile 2 -> (3, 1), tile 2 -> (1, 1), tile 3 -> (1, 4), tile -2 -> (1, 2), tile -1 -> (2, 2), tile 0

Conclusion

The Schönbrunn maze puzzle is a fun brain teaser, yet quite simple.

It can be a very good warmup puzzle for a typical MathsJam session for instance!

We saw how to solve it in two ways, manually and with a program. The program runs fast because the size of the problem is rather small.

A few questions open up from that:

• Is this puzzle part of bigger family of puzzles? Does it have a name? It would be very interesting to know.
• Is it possible to generate different configurations (input) that have a solution?
• Are there versions of this puzzle with bigger boards?

Feel free to share your thoughts.

Hope you enjoyed it!